Contact geometry

Contact geometry deals with certain manifolds of odd dimension. It is close to symplectic geometry and like the latter, it originated in questions of classical mechanics. A contact structure on a (2n+1)-dimensional manifold M is given by a smooth hyperplane field H in the tangent bundle that is as far as possible from being associated with the level sets of a differentiable function on M (the technical term is "completely nonintegrable tangent hyperplane distribution"). Near each point p, a hyperplane distribution is determined by a nowhere vanishing 1-form α, which is unique up to multiplication by a nowhere vanishing function:



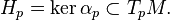
A local 1-form on M is a contact form if the restriction of its exterior derivative to H is a non-degenerate 2-form and thus induces a symplectic structure on Hp at each point. If the distribution H can be defined by a global 1-form α then this form is contact if and only if the top-dimensional form




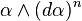
is a volume form on M, i.e. does not vanish anywhere. A contact analogue of the Darboux theorem holds: all contact structures on an odd-dimensional manifold are locally isomorphic and can be brought to a certain local normal form by a suitable choice of the coordinate system.

Taken From http://en.wikipedia.org/wiki/Differential_geometry