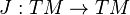Complex and Kähler geometry

Complex differential geometry is the study of complex manifolds. An almost complex manifold is a real manifold M, endowed with a tensor of type (1,1), i.e. a vector bundle endomorphism (called an almost complex structure)

, such that J2 = − 1.

It follows from this definition that an almost complex manifold is even dimensional.
An almost complex manifold is called complex if NJ = 0, where NJ is a tensor of type (2,1) related to J, called the Nijenhuis tensor (or sometimes the torsion). An almost complex manifold is complex if and only if it admits a holomorphic coordinate atlas. An almost Hermitian structure is given by an almost complex structure J, along with a riemannian metric g, satisfying the compatibility condition g(JX,JY) = g(X,Y). An almost hermitian structure defines naturally a differential 2-form ωJ,g(X,Y): = g(JX,Y). The following two conditions are equivalent:
1. NJ = 0 and dω = 0,
2.
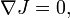
where is the Levi-Civita connection of g. In this case, (J,g) is called a Kähler structure, and a Kähler manifold is a manifold endowed with a Kähler structure. In particular, a Kähler manifold is both a complex and a symplectic manifold. A large class of Kähler manifolds (the class of Hodge manifolds) is given by all the smooth complex projective varieties.

Taken From http://en.wikipedia.org/wiki/Differential_geometry