Finsler geometry has the Finsler manifold as the main object of study — this is a differential manifold with a Finsler metric, i.e. a Banach norm defined on each tangent space. A Finsler metric is a much more general structure than a Riemannian metric. A Finsler structure on a manifold M is a function F : TM → [0,∞) such that:
1. F(x, my) = |m|F(x,y) for all x, y in TM,
2. F is infinitely differentiable in TM − {0},
3. The vertical Hessian of F2 is positive definite.
Taken From http://en.wikipedia.org/wiki/Differential_geometry
Riemannian geometry
| By Calculus for All
Riemannian geometry studies Riemannian manifolds, smooth manifolds with a Riemannian metric, a notion of a distance expressed by means of a smooth positive definite symmetri bilinear form defined on the tangent space at each point. Riemannian geometry generalizes Euclidean geometry to spaces that are not necessarily flat, although they still resemble the Euclidean space at each point "infinitesimally", i.e. in the first order of approximation. Various concepts based on length, such as the arc length of curves, area of plane regions, and volume of solids all admit natural analogues in Riemannian geometry. The notion of a directional derivative of a function from multivariable calculus is extended in Riemannian geometry to the notion of a covariant derivative of a tensor. Many concepts and techniques of analysis and differential equations have been generalized to the setting of Riemannian manifolds.
A distance-preserving diffeomorphism between Riemannian manifolds is called an isometry. This notion can also be defined locally, i.e. for small neighborhoods of points. Any two regular curves are locally isometric. However, Theorema Egregium of Gauss showed that already for surfaces, the existence of a local isometry imposes strong compatibility conditions on their metrics: the Gaussian curvatures at the corresponding points must be the same. In higher dimensions, the Riemann curvature tensor is an important pointwise invariant associated to a Riemannian manifold that measures how close it is to being flat. An important class of Riemannian manifolds is formed by the Riemannian symmetric spaces, whose curvature is not necessarily constant. They are the closest to the "ordinary" plane and space considered in Euclidean and non-Euclidean geometry.
Taken From http://en.wikipedia.org/wiki/Differential_geometry
A distance-preserving diffeomorphism between Riemannian manifolds is called an isometry. This notion can also be defined locally, i.e. for small neighborhoods of points. Any two regular curves are locally isometric. However, Theorema Egregium of Gauss showed that already for surfaces, the existence of a local isometry imposes strong compatibility conditions on their metrics: the Gaussian curvatures at the corresponding points must be the same. In higher dimensions, the Riemann curvature tensor is an important pointwise invariant associated to a Riemannian manifold that measures how close it is to being flat. An important class of Riemannian manifolds is formed by the Riemannian symmetric spaces, whose curvature is not necessarily constant. They are the closest to the "ordinary" plane and space considered in Euclidean and non-Euclidean geometry.
Taken From http://en.wikipedia.org/wiki/Differential_geometry
Symplectic geometry
| By Calculus for All
Symplectic geometry is the study of symplectic manifolds. An almost symplectic manifold is a differentiable manifold equipped with a smoothly varying non-degenerate skew-symmetric bilinear form on each tangent space, i.e., a nondegenerate 2-form ω, called the symplectic form. A symplectic manifold is an almost symplectic manifold for which the symplectic form ω is closed: dω = 0.
A diffeomorphism between two symplectic manifolds which preserves the symplectic form is called a symplectomorphism. Non-degenerate skew-symmetric bilinear forms can only exist on even dimensional vector spaces, so symplectic manifolds necessarily have even dimension. In dimension 2, a symplectic manifold is just a surface endowed with an area form and a symplectomorphism is an area-preserving diffeomorphism. The phase space of a mechanical system is a symplectic manifold and they made an implicit appearance already in the work of Lagrange on analytical mechanics and later in Jacobi's and Hamilton's formulation of classical mechanics.
By contrast with Riemannian geometry, where the curvature provides a local invariant of Riemannian manifolds, Darboux's theorem states that all symplectic manifolds are locally isomorphic. The only invariants of a symplectic manifold are global in nature and topological aspects play a prominent role in symplectic geometry. The first result in symplectic topology is probably the Poincaré-Birkhoff theorem, conjectured by Henri Poincaré and proved by George Birkhoff in 1912. It claims that if an area preserving map of an annulus twists each boundary component in opposite directions, then the map has at least two fixed points.
Taken From http://en.wikipedia.org/wiki/Differential_geometry
A diffeomorphism between two symplectic manifolds which preserves the symplectic form is called a symplectomorphism. Non-degenerate skew-symmetric bilinear forms can only exist on even dimensional vector spaces, so symplectic manifolds necessarily have even dimension. In dimension 2, a symplectic manifold is just a surface endowed with an area form and a symplectomorphism is an area-preserving diffeomorphism. The phase space of a mechanical system is a symplectic manifold and they made an implicit appearance already in the work of Lagrange on analytical mechanics and later in Jacobi's and Hamilton's formulation of classical mechanics.
By contrast with Riemannian geometry, where the curvature provides a local invariant of Riemannian manifolds, Darboux's theorem states that all symplectic manifolds are locally isomorphic. The only invariants of a symplectic manifold are global in nature and topological aspects play a prominent role in symplectic geometry. The first result in symplectic topology is probably the Poincaré-Birkhoff theorem, conjectured by Henri Poincaré and proved by George Birkhoff in 1912. It claims that if an area preserving map of an annulus twists each boundary component in opposite directions, then the map has at least two fixed points.
Taken From http://en.wikipedia.org/wiki/Differential_geometry
Complex and Kähler geometry
| By Calculus for All
Complex differential geometry is the study of complex manifolds. An almost complex manifold is a real manifold M, endowed with a tensor of type (1,1), i.e. a vector bundle endomorphism (called an almost complex structure)
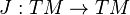, such that J2 = − 1.
It follows from this definition that an almost complex manifold is even dimensional.
An almost complex manifold is called complex if NJ = 0, where NJ is a tensor of type (2,1) related to J, called the Nijenhuis tensor (or sometimes the torsion). An almost complex manifold is complex if and only if it admits a holomorphic coordinate atlas. An almost Hermitian structure is given by an almost complex structure J, along with a riemannian metric g, satisfying the compatibility condition g(JX,JY) = g(X,Y). An almost hermitian structure defines naturally a differential 2-form ωJ,g(X,Y): = g(JX,Y). The following two conditions are equivalent:
1. NJ = 0 and dω = 0,
2.
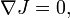
where
is the Levi-Civita connection of g. In this case, (J,g) is called a Kähler structure, and a Kähler manifold is a manifold endowed with a Kähler structure. In particular, a Kähler manifold is both a complex and a symplectic manifold. A large class of Kähler manifolds (the class of Hodge manifolds) is given by all the smooth complex projective varieties.
Taken From http://en.wikipedia.org/wiki/Differential_geometry
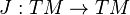, such that J2 = − 1.It follows from this definition that an almost complex manifold is even dimensional.
An almost complex manifold is called complex if NJ = 0, where NJ is a tensor of type (2,1) related to J, called the Nijenhuis tensor (or sometimes the torsion). An almost complex manifold is complex if and only if it admits a holomorphic coordinate atlas. An almost Hermitian structure is given by an almost complex structure J, along with a riemannian metric g, satisfying the compatibility condition g(JX,JY) = g(X,Y). An almost hermitian structure defines naturally a differential 2-form ωJ,g(X,Y): = g(JX,Y). The following two conditions are equivalent:
1. NJ = 0 and dω = 0,
2.
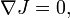
where
is the Levi-Civita connection of g. In this case, (J,g) is called a Kähler structure, and a Kähler manifold is a manifold endowed with a Kähler structure. In particular, a Kähler manifold is both a complex and a symplectic manifold. A large class of Kähler manifolds (the class of Hodge manifolds) is given by all the smooth complex projective varieties.Taken From http://en.wikipedia.org/wiki/Differential_geometry
Contact geometry
| By Calculus for All
Contact geometry deals with certain manifolds of odd dimension. It is close to symplectic geometry and like the latter, it originated in questions of classical mechanics. A contact structure on a (2n+1)-dimensional manifold M is given by a smooth hyperplane field H in the tangent bundle that is as far as possible from being associated with the level sets of a differentiable function on M (the technical term is "completely nonintegrable tangent hyperplane distribution"). Near each point p, a hyperplane distribution is determined by a nowhere vanishing 1-form α, which is unique up to multiplication by a nowhere vanishing function:
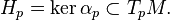
A local 1-form on M is a contact form if the restriction of its exterior derivative to H is a non-degenerate 2-form and thus induces a symplectic structure on Hp at each point. If the distribution H can be defined by a global 1-form α then this form is contact if and only if the top-dimensional form
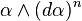
is a volume form on M, i.e. does not vanish anywhere. A contact analogue of the Darboux theorem holds: all contact structures on an odd-dimensional manifold are locally isomorphic and can be brought to a certain local normal form by a suitable choice of the coordinate system.
Taken From http://en.wikipedia.org/wiki/Differential_geometry
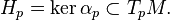
A local 1-form on M is a contact form if the restriction of its exterior derivative to H is a non-degenerate 2-form and thus induces a symplectic structure on Hp at each point. If the distribution H can be defined by a global 1-form α then this form is contact if and only if the top-dimensional form
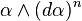
is a volume form on M, i.e. does not vanish anywhere. A contact analogue of the Darboux theorem holds: all contact structures on an odd-dimensional manifold are locally isomorphic and can be brought to a certain local normal form by a suitable choice of the coordinate system.
Taken From http://en.wikipedia.org/wiki/Differential_geometry
Taylor polynomials and Taylor series
| By Calculus for All
The derivative gives the best possible linear approximation, but this can be very different from the original function. One way of improving the approximation is to take a quadratic approximation. That is to say, the linearization of a real-valued function f(x) at the point x0 is a linear polynomial a + b(x - x0), and it may be possible to get a better approximation by considering a quadratic polynomial a + b(x - x0) + c(x - x0)². Still better might be a cubic polynomial a + b(x - x0) + c(x - x0)² + d(x - x0)³, and this idea can be extended to arbitrarily high degree polynomials. For each one of these polynomials, there should be a best possible choice of coefficients a, b, c, and d that makes the approximation as good as possible.
For a, the best possible choice is always f(x0), and for b, the best possible choice is always f'(x0). For c, d, and higher-degree coefficients, these coefficients are determined by higher derivatives of f. c should always be f''(x0)/2, and d should always be f'''(x0)/3!. Using these coefficients gives the Taylor polynomial of f. The Taylor polynomial of degree d is the polynomial of degree d which best approximates f, and its coefficients can be found by a generalization of the above formulas. Taylor’s theorem gives a precise bound on how good the approximation is. If f is a polynomial of degree less than or equal to d, then the Taylor polynomial of degree d equals f.
The limit of the Taylor polynomials is an infinite series called the Taylor series. The Taylor series is frequently a very good approximation to the original function. Functions which are equal to their Taylor series are called analytic functions . It is impossible for functions with discontinuities or sharp corners to be analytic, but there are smooth functions which are not analytic.
Taken From http://en.wikipedia.org/wiki/Differential_calculus#Calculus_of_variations
For a, the best possible choice is always f(x0), and for b, the best possible choice is always f'(x0). For c, d, and higher-degree coefficients, these coefficients are determined by higher derivatives of f. c should always be f''(x0)/2, and d should always be f'''(x0)/3!. Using these coefficients gives the Taylor polynomial of f. The Taylor polynomial of degree d is the polynomial of degree d which best approximates f, and its coefficients can be found by a generalization of the above formulas. Taylor’s theorem gives a precise bound on how good the approximation is. If f is a polynomial of degree less than or equal to d, then the Taylor polynomial of degree d equals f.
The limit of the Taylor polynomials is an infinite series called the Taylor series. The Taylor series is frequently a very good approximation to the original function. Functions which are equal to their Taylor series are called analytic functions . It is impossible for functions with discontinuities or sharp corners to be analytic, but there are smooth functions which are not analytic.
Taken From http://en.wikipedia.org/wiki/Differential_calculus#Calculus_of_variations
Mean value theorem
| By Calculus for All
The mean value theorem gives a relationship between values of the derivative and values of the original function. If f(x) is a real-valued function and a and b are numbers with a < b, then the mean value theorem says that under mild hypotheses, the slope between the two points (a, f(a)) and (b, f(b)) is equal to the slope of the tangent line to f at some point c between a and b. In other words,
In practice, what the mean value theorem does is control a function in terms of its derivative. For instance, suppose that f has derivative equal to zero at each point. This means that its tangent line is horizontal at every point, so the function should also be horizontal. The mean value theorem proves that this must be true: The slope between any two points on the graph of f must equal the slope of one of the tangent lines of f. All of those slopes are zero, so any line from one point on the graph to another point will also have slope zero. But that says that the function does not move up or down, so it must be a horizontal line. More complicated conditions on the derivative lead to less precise but still highly useful information about the original function.
Taken From http://en.wikipedia.org/wiki/Differential_calculus#Calculus_of_variations
In practice, what the mean value theorem does is control a function in terms of its derivative. For instance, suppose that f has derivative equal to zero at each point. This means that its tangent line is horizontal at every point, so the function should also be horizontal. The mean value theorem proves that this must be true: The slope between any two points on the graph of f must equal the slope of one of the tangent lines of f. All of those slopes are zero, so any line from one point on the graph to another point will also have slope zero. But that says that the function does not move up or down, so it must be a horizontal line. More complicated conditions on the derivative lead to less precise but still highly useful information about the original function.
Taken From http://en.wikipedia.org/wiki/Differential_calculus#Calculus_of_variations
Physics
| By Calculus for All
Physics
Calculus is of vital importance in physics: many physical processes are described by equations involving derivatives, called differential equations . Physics is particularly concerned with the way quantities change and evolve over time, and the concept of the "time derivative" — the rate of change over time — is essential for the precise definition of several important concepts. In particular, the time derivatives of an object's position are significant in Newtonian physics:
• Velocity is the derivative (with respect to time) of an object's displacement (distance from the original position)
• Acceleration is the derivative (with respect to time) of an object's velocity, that is, the second derivative (with respect to time) of an object's position.
For example, if an object's position on a line is given by
then the object's velocity is
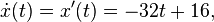
and the object's acceleration is
which is constant.
Taken From http://en.wikipedia.org/wiki/Differential_calculus#Calculus_of_variations
Calculus is of vital importance in physics: many physical processes are described by equations involving derivatives, called differential equations . Physics is particularly concerned with the way quantities change and evolve over time, and the concept of the "time derivative" — the rate of change over time — is essential for the precise definition of several important concepts. In particular, the time derivatives of an object's position are significant in Newtonian physics:
• Velocity is the derivative (with respect to time) of an object's displacement (distance from the original position)
• Acceleration is the derivative (with respect to time) of an object's velocity, that is, the second derivative (with respect to time) of an object's position.
For example, if an object's position on a line is given by
then the object's velocity is
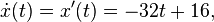
and the object's acceleration is
which is constant.
Taken From http://en.wikipedia.org/wiki/Differential_calculus#Calculus_of_variations
Differential equations
| By Calculus for All
Main article: Differential Equation
A differential equation is relation between a collection of functions and their derivatives. An ordinary differential equation is a differential equation that relates functions of one variable to their derivatives with respect to that variable. A partial differential equation is a differential equation that relates functions of more than one variable to their partial derivatives. Differential equations arise naturally in the physical sciences, in mathematical modelling, and within mathematics itself. For example, Newton Seconds Law , which describes the relationship between acceleration and position, can be stated as the ordinary differential equation
The heat equation in one space variable, which describes how heat diffuses through a straight rod, is the partial differential equation
Here u(x, t) is the temperature of the rod at position x and time t and α is a constant that depends on how fast heat diffuses through the rod.
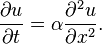
Taken From http://en.wikipedia.org/wiki/Differential_calculus
A differential equation is relation between a collection of functions and their derivatives. An ordinary differential equation is a differential equation that relates functions of one variable to their derivatives with respect to that variable. A partial differential equation is a differential equation that relates functions of more than one variable to their partial derivatives. Differential equations arise naturally in the physical sciences, in mathematical modelling, and within mathematics itself. For example, Newton Seconds Law , which describes the relationship between acceleration and position, can be stated as the ordinary differential equation
The heat equation in one space variable, which describes how heat diffuses through a straight rod, is the partial differential equation
Here u(x, t) is the temperature of the rod at position x and time t and α is a constant that depends on how fast heat diffuses through the rod.
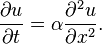
Taken From http://en.wikipedia.org/wiki/Differential_calculus
The derivative
| By Calculus for All
The derivative
Main article: Derivative
Suppose that x and y are real numbers and that y is a function of x, that is, for every value of x, we can determine the value of y. This relationship is written as: y = f(x). Where f(x) is the equation for a straight line, y = m x + b, where m and b are real numbers that determine the locus of the line in Cartesian coordinates. m is called the slope and is given by:
where the symbol Δ (the uppercase form of the Greek letter Delta) is an abbreviation for "change in". It follows that Δy = m Δx.
In linear functions the derivative of f at the point x is the best possible approximation to the idea of the slope of f at the point x. It is usually denoted f'(x) or dy/dx. Together with the value of f at x, the derivative of f determines the best linear approximation, or linearization, of f near the point x. This latter property is usually taken as the definition of the derivative. Derivatives cannot be calculated in nonlinear functions because they do not have a well-defined slope.
A closely related notion is the differential of a function.
The tangent line at (x, f(x))
When x and y are real variables, the derivative of f at x is the slope of the tangent line to the graph of f' at x. Because the source and target of f are one-dimensional, the derivative of f is a real number. If x and y are vectors, then the best linear approximation to the graph of f depends on how f changes in several directions at once. Taking the best linear approximation in a single direction determines a partial derivative, which is usually denoted ∂y/∂x. The linearization of f in all directions at once is called the total derivative. It is a linear transformation, and it determines the hyperplane that most closely approximates the graph of f. This hyperplane is called the oscilating hyperplane; it is conceptually the same idea as taking tangent lines in all directions at once.
taken from http://en.wikipedia.org/wiki/Differential_calculus